◁◁◁

Тематические серии:

• решение уравнений: А-8, А-12, А-9, А-15, А-110
• решение уравнений с целой и дробной частями числа: А-40, А-46, А-47, А-48, А-49, А-50, А-53, А-52, А-51
• решение систем уравнений: А-61, А-59, А-112, А-113, А-114, А-115, А-116, А-117, А-60
• построение графика функции: А-4, А-5, А-70, А-74, А-63, А-44, А-65
• построение графиков (выражения с обратными тригонометрическими функциями): А‑32, А-33, А-31, А-62, А-34, А-38, А-58, А-57
• построение графика функции, выражение которой содержит дробную часть числа: А-17, А-39, А-18, А-19, А-20, А-21, А-22
• построение графика функции, выражение которой содержит целую часть числа: А-35, А‑36, А-37, А-39
• построение графика уравнения: А-11, А-25, А-121, А-122, А-111, А-75, А-107, А-1, А-23, А-24, А-118, А-120, А-119
• построение графика уравнения вида f(y) = f(x): А-16, А-83, А-82, А-81, А-80, А-10, А-26, А-79, А-29, А-30, А-78, А-77, А-76
• построение графика уравнения вида f(y)·f(x) = k : А-84, А-85, А-86, А-87, А-88, А-89, А‑90, А-91, А-92, А-93, А-95, А-96, А-97, А-98, А-99, А-100
• построение графика неравенства: А-27, А-54, А-55, А-67, А-66, А-109
• построение множества точек, координаты которых удовлетворяют набору условий: А-6, А-94, А-2, А-3, А-7, А-28
• вычисление значения интеграла: А-41, А-42, А-45, А-69, А-71
• доказательство тождеств: А-56, А-101, А-102, А-108
• подбор коэффициентов в выражении функции с известным графиком: А-103, А-106, А-104, А-105
• разные задачи: А-73, А-72, А-13, А-14, А-43, А-64, А-68

А-1. Изoбpaзитe нa кoopдинaтнoй плocкocти мнoжecтвo тoчeк, кoopдинaты кoтopыx yдoвлeтвopяют ypaвнeнию:

x² + y² = |2x| + |2y| – 1

А-2. Изобразите на плоскости множество точек, координаты которых удовлетворяют системе неравенств:

А-3. Дана система неравенств:

а) Изобразите на плоскости множество точек, координаты которых удовлетворяют данной системе.

б) Определите у получившейся фигуры координаты точек, наиболее удалённых от начала координат.

А-4. Построить график функции:

А-5. Построить график функции:

y = | |x| – 1 | – (|x| – 1)

А-6. Изобразите на плоскости множество точек, координаты которых удовлетворяют следующей системе неравенств:

А-7. Изобразите на плоскости множество точек, координаты которых удовлетворяют следующему набору условий:

А-8. Решите уравнение:

3x|x| – 28 = 6

А-9. Решите уравнение:

cos⁴ x – 1 111·cos³ x – 112 110·sin² x – 1 111 000·cos x + 1 112 110 = 0

А-10. Построить график уравнения:

sin x = sin y

А-11. Построить график уравнения:

|y| = sin x

А-12. Решите уравнение:

e^4x + = ( + 1)·e^2x

А-13. Найти значение выражения, если n – натуральное, а m – целое:

А-14. Разложить на множители: m⁵ + m⁴n + m³n² + m²n³ + mn⁴ + n⁵

А-15. Найти все корни уравнения: z⁵ + 2z⁴ + 4z³ + 8z² + 16z⁴ + 32 = 0

А-16. Изобразить множество точек, координаты которых удовлетворяют условию:

y² = x²

А-17. Дробная часть числа x обозначается как {x}. Данная функция определена на всём множестве действительных чисел, область её значений – полуинтервал [0; 1), кроме того, она является периодической функцией с периодом, равным 1. С учётом этих данных построить график функции

y = |{x} – ¹/₂|

А-18. Построить график функции

y = |{x}² – ¹/₂|

А-19. Построить график функции

А-20. Построить график функции

А-21. Построить график функции

А-22. Построить график функции

А-23. Построить график уравнения:

{x} = {x}² + y²

А-24. Построить график уравнения:

y² = ({x} – ¹/₂)²

А-25. Построить график уравнения:

y² = sin⁴x

А-26. Построить график уравнения:

tg y = tg x

А-27. Изобразите на плоскости множество точек, координаты которых соответствуют требованию:

|y| ≤ sin²x + 1

А-28. Изобразить на плоскости множество точек, координаты которых удовлетворяют системе неравенств:

А-29. Построить график уравнения:

{y} = {x}

А-30. Целая часть числа x обозначается как [x]. Под ней понимается наибольшее целое число, не превышающее заданное. Функция y = [x] определена на всём множестве действительных чисел. С учётом этих данных построить график уравнения:

[y] = [x]

А-31. Построить график функции:

y = arcsin(sin x)

А-32. Построить график функции:

y = arccos(cos x)

А-33. Построить график функции:

y = arctg(tg x)

А-34. Построить график функции:

y = arcsin(sin x) + arccos(cos x)

А-35. Построить график функции:

y = [x]²

А-36. Построить график функции:

y = [x²]

А-37. Построить график функции:

y = [sin x]

А-38. Построить график функции:

y = arctg(tg x) – arcctg(ctg x)

А-39. Под целой частью числа x (обозначается при помощи квадратных скобок [x]) понимается наибольшее целое число, не превышающее заданное. Дробная часть x обозначается фигурными скобками и определяется как разность между самим числом и его целой частью: {x} = x – [x] . Область определения функций y = [x] и y = {x} – всё множество действительных чисел, к тому же y = {x} является периодической функцией с периодом, равным 1, а область её значений – полуинтервал [0; 1). На основании данной информации построить график функции:

y = [{x} – ¹/₂]

А-40. Решите уравнение:

[x] = [x]²

А-43. Решите неравенство:

А-44. Построить график функции:

А-45. Найти значение интеграла:

Даны два действительных числа a и b, такие, что a < b. Решите уравнение:

А-46.

А-47.

Решите уравнение:

А-48.

44[x]{x}=[x]

А-49.

5{x}² – 28{x} + 15 = 0

А-50.

[x² + 2x – 3] + 4 = 0

А-51.

[x² + 2|x| – 3] = 4

А-52.

[3{x}² + 8{x} – 3] = 0

А-53.

4[x]{x} + 4 = x + 15{x}

Изобразите на плоскости множество точек, координаты которых соответствуют требованию:

А-54.

|y| ≤ sin(arcsin x) + 1

А-55.

|y| ≤ cos(arccos(|x| + ¹/₃))

А-56. Доказать, что при x ∈ [–1; 1] выполняется тождество:

sin(arccos x) = cos(arcsin x)

Построить график функции:

А-57.

y = cos(arcsin(sin x))

А-58.

y = sin(arccos(cos x))

А-59. Решите систему уравнений:

А-60. Каким условиям должны удовлетворять действительные числа a, b, c и d, чтобы система уравнений

имела ровно два решения?

А-61. Найдите точки плоскости, координаты которых удовлетворяют следующим условиям:

x² + x – 2 = 0   и   y² – 2y – 3 = 0

А-62. Построить график функции, если a > 1:

y(x) = a·sin(arcsin(x/a))

А-63. Построить график функции:

y = 1 + |x|·(| |x| – 1 | – 1)

А-64. При каких значения параметра a неравенство

|x|·(| |x| – 1 | – 1) ≥ a

выполняется при любом значении x?

А-65. Построить график функции:

Изобразите на плоскости множество точек, координаты которых соответствуют требованию:

А-66.

А-67.

А-68. Найдите площадь фигуры, образуемой точками на плоскости, координаты которых удовлетворяют следующему условию:

А-69. Найти значение интеграла

А-70. Построить график функции

А-71. Найти значение интеграла

А-72. Функция y = f(x) определена на интервале (a; b). Найдите область определения функции y = f(|x|) и опишите, как будет выглядеть её график, если: а) 0 < a < b ; б) a < 0 < b .

А-73. Функция y = f(x) определена на интервале (a; b). Найдите область определения функции

и опишите, как будет выглядеть её график, если a < 0 < b .

А-74. Построить график функции (a – постоянное действительное число):

А-75. Построить график уравнения, если a, b – постоянные числа и a < b :

А-76. Функция «гиперболический синус» обозначается как sh t и определяется так:

Построить на координатной плоскости график уравнения

sh y = sh x

А-77. Функция «гиперболический косинус» обозначается как ch t и определяется так:

Построить на координатной плоскости график уравнения

ch y = ch x

А-78. Функция знака числа, называемая также «сигнум», определена для любого действительного аргумента t. Обозначается она как sgn t и принимает нулевое значение при t = 0, а при положительных и отрицательных значениях аргумента сигнум равен 1 и –1 соответственно. На основании этих сведений построить на координатной плоскости график уравнения

sgn y = sgn x

А-79. Функцию «секанс» обычно определяют как величину, обратную косинусу:

Построить на координатной плоскости график уравнения

sec y = sec x

Построить на координатной плоскости график уравнения:

А-80.

yⁿ = xⁿ ,

если: а) n = 2k ; б) n = 2k – 1 ; в) n = –2k ; г) n = 1 – 2k (k – натуральное число).

А-81.

,

если: а) n = 2k ; б) n = 2k + 1 (k – натуральное число).

А-82.

arcsin y = arcsin x

А-83.

log_a y = log_a x   (a > 0, a ≠ 1)

А-84.

e^y·e^x = 1

А-85.

yⁿ·xⁿ = 0   (n > 0):

А-86.

arcsin y · arcsin x = 0

А-87.

arccos y · arccos x = 0

А-88.

log_a y · log_a x = 0   (a > 0, a ≠ 1)

А-89.

arccos |y| · arccos |x| = 0

А-90.

sh y · sh x = 0

А-91.

cos y · cos x = 0

А-92.

{y}·{x} = 0

А-93.

[y]·[x] = 0

А-94. Изобразить на плоскости множество точек, координаты которых удовлетворяют системе (m, n – целые числа):

Построить на координатной плоскости график уравнения:

А-95.

tg y · tg x = 0

А-96.

[y]·[x] = 1

А-97.

sgn y · sgn x = k ,

если: а) k = 0; б) k = 1 ; в) k = –1 .

А-98.

[y]·[x] = k ,

где k – простое число.

А-99.

[y]·[x] = 4

А-100.:

[|y|]·[|x|] = 3

Докажите, что для любого действительного x выполняется тождество

А-101.

|x + 1| + |x – 1| – |x| – 1 = | |x| – 1 |

А-102.

А-103. На рисунке изображён график функции (M, N – положительные величины):

Он пересекает ось абсцисс в точках (–a; 0) и (a; 0). а в точке (0; b) имеет максимум. Выразите значения коэффициентов M и N через числа a и b.

А-104. На рисунке изображён график функции (A, B, C – положительные величины):

Он пересекает ось абсцисс в точках (–m; 0) и (m; 0), а на отрезке значений аргумента [–n; n] параллелен оси абсцисс – там y(x) имеет постоянное значение, равное k. Выразите величины коэффициентов A. B и C через числа m, n, k.

А-105. На рисунке изображён график функции (A, B, C, D – положительные величины):

Он представляет собой непрерывную ломаную линию, пересекающую ось абсцисс в точках (–m; 0) и (m; 0). Точки «излома» графика имеют координаты (–n; k), (n; k) и (0; p), причём последняя является максимумом y(x). Выразите величины коэффициентов A. B, C и D через числа m, n, k, p.

А-106. На рисунке изображён график функции:

Он пересекает ось абсцисс в точках (a; 0) и (c; 0). а в точке (0; b) имеет максимум. Выразите значения коэффициентов M, N, K через числа a, b, c.

А-107. Построить на координатной плоскости график уравнения:

(y + 2/π·arcsin x)·(y² + x² – 2x) = 0

А-108. Докажите, что при x ∈ [–2; 1) выполняется тождество

А-109. Изобразите на плоскости множество точек, координаты которых соответствуют требованию:

(x² + y² – 4)·(|x| + |y| – 1) ≤ 0

А-110. Решите уравнение:

ch x · ch y = 1

А-111. Постройте график уравнения:

(|x + y| – 1)·(|x – y| – 1) = 0

Решите систему уравнений:

А-112.

А-113.

А-114.

А-115.

А-116.

А-117.

Изобразите на координатной плоскости график уравнения:

А-118.

А-119.

А-120.

А-121.

sin(πx² + πy²) = 0

А-122.

{x² + y²} = 0

Примечание: при описании решений некоторых задач для лаконичности применяется подход с использованием равносильных преобразований. Так как не всем учащимся в школе рассказывают о принятой для этого символике, к ознакомлению рекомендуется специально посвящённая данной теме публикация.

Добавлено: 14.08.2019

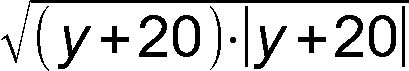
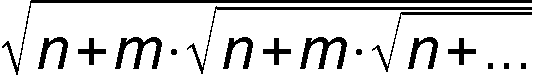
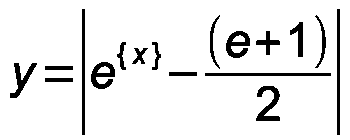
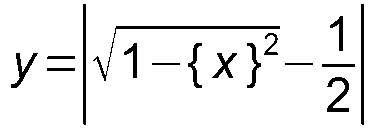
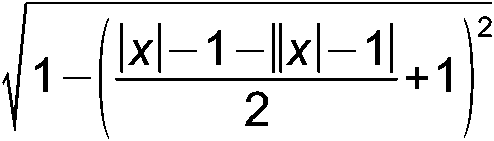
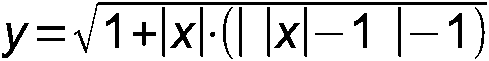
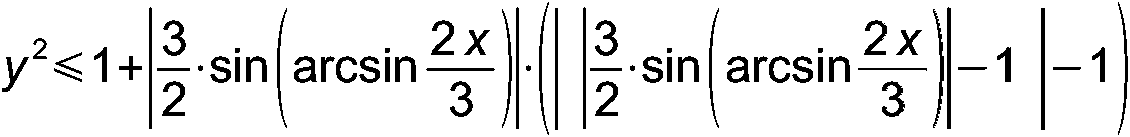
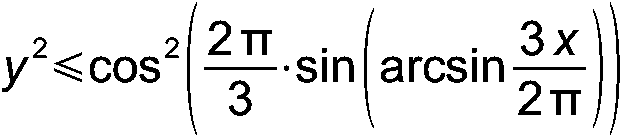
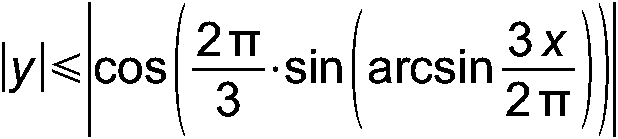
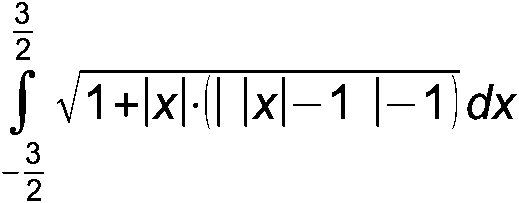
Изменено: 31.05.2026