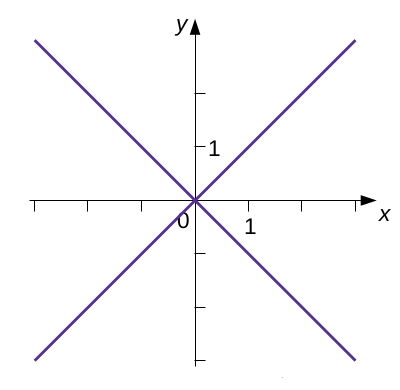
Две серии задач для школьников: про общие черты в ответах к ним

На сайте в разделе «Школьные задачи» опубликованы две серии заданий по алгебре, где рассматривается построение графиков уравнений вида f(y) = f(x) и f(y)·f(x) = k (в качестве k чаще встречается ноль, но не только). Данные упражнения сравнительно простые, хотя некоторое «спотыкание» у учащихся могут вызвать задачи, где фигурируют обычно не рассматриваемые в школьном курсе функции типа сигнума sgn t (знак числа t), но при формулировании таких заданий обязательно даются разъяснения, позволяющие с решением справиться. Если же окинуть взглядом получающиеся в итоге картинки (графики), то неизбежно становятся заметны некоторые общности в их виде, хотя в силу того, что рассматриваются самые разные функции, единых черт на самом деле совсем немного, тем не менее их стоит кратко описать.

Одна группа упражнений – f(y) = f(x) – представлена следующими задачами (в порядке нарастания сложности):

А-16, А-83, А-82, А-81, А-80, А-10, А-26, А-79, А-29, А-30, А-78, А-77, А-76.

Другая ( f(y)·f(x) = k ) содержит такие задания:

А-84, А-85, А-86, А-87, А-88, А-89, А‑90, А‑91, А-92,
А-93, А-95, А-96, А-97, А-98, А-99, А-100.

Первое общее, что может броситься в глаза – графики уравнений в массе своей довольно унылы – это всего лишь небольшое число прямых линий или их частей. Причина этого заключена, как мне кажется, в самой простоте вида уравнений (рис. 1, 2).

А-16: x² = y² ;
А-77: ch y = ch x ;
А-80: yⁿ = xⁿ (n = 2k, k ∈ ℕ)

Рис. 1.

А-85: yⁿ·xⁿ = 0 (n > 0);
А-90: sh x · sh x = 0 ;
А-97: sgn y · sgn x = 0

Рис. 2.

Исключения, которые «унылыми» назвать уже сложнее, имеются, причём в достатке – это, прежде всего, уравнения с сигнумом и антье (целой частью числа), описывающие на плоскости не отдельные линии, а целые области (рис. 3, 4).

А-30: [y] = [x]

Рис. 3.

А-97: sgn y · sgn x = 1

Рис. 4.

Кроме того, выделяются и уравнения, содержащие тригонометрические функции и функцию дробной части числа – в силу своей периодичности они описывают совокупности бесконечного числа прямых линий, в том числе – совокупности, образующие на плоскости «сетки», и являются, на мой взгляд, интересными примерами, дополняющими опубликованную ранее заметку (рис. 5, 6).

А-91: cos y · cos x = 0

Рис. 5.

А-92: {y}·{x} = 0

Рис. 6.

Таким образом, первое сформулированное обобщение не является универсальным, более того – можно легко подобрать функции для уравнения вида f(y)·f(x) = k , график которого содержит действительно кривые линии. В качестве подтверждающего это примера, не рассматривавшегося в виде отдельно опубликованного разбора задачи можно привести уравнение

Вид этого равенства исключает из множества решений уравнения такие, где x = 0 или y = 0, но благодаря этому становится допустимо следующее равносильное преобразование:

Строится график такого уравнения довольно просто (рис. 7): берём график функции y = 1/x (а он представляет собой гиперболу), отражаем симметрично оси абсцисс в верхнюю полуплоскость его часть, находящуюся в третьем квадранте – при этом получается график функции y = 1/|x| , а затем то, что получилось, дублируем, отражая уже из верхней полуплоскости в нижнюю симметрично горизонтальной координатной оси (см. комментарий к заданию А-25).

Рис. 7.

Второй и на этот раз действительно общей особенностью графиков является их симметрия относительно линии y = x (а в отдельных случаях ещё и относительно y = –x). Любопытно, что для уравнения f(y)·f(x) = k симметрия эта склонна нарушаться для многих функций, если выбрать k отличным от нуля или единицы, однако на антье, судя по обсуждаемым задачам, это не распространяется (рис. 8), как и на вариант sgn y · sgn x = –1 (рис. 9).

А-98: [y]·[x] = k (k – простое число)

Рис. 8.

А-97: sgn y · sgn x = –1

Рис. 9.

Заканчивая заметку, остаётся лишь отметить, что описанное выше – просто наблюдение, для подытоживания результатов рассматриваемых серий задач, без попытки сделать какие-либо далеко идущие выводы.