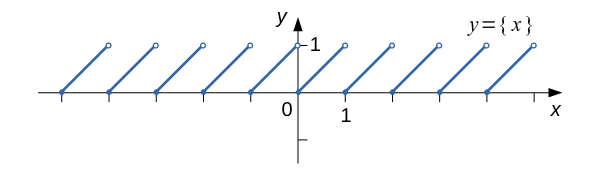
Тот, кто хорошо помнит школьную математику, легко сможет назвать функции, обладающие свойством периодичности – синус, косинус, тангенс и котангенс. Некоторые, возможно, припомнят, что ещё есть секанс и косеканс.

Существует, однако, функция, тоже обладающая периодичностью, но к тригонометрическим, как перечисленные выше, не относящаяся. Про неё иногда школьникам рассказывают на уроках – это дробная часть числа y = {x} . Я некоторое время назад «игрался» с этой функцией, получив в итоге целую россыпь интересных (ну, по крайней мере, мне они таковыми кажутся) задач для школьников, которые опубликованы на сайте и дзен-канале. При этом сложно было не подметить некоторую взаимосвязь {x} с тригонометрией, вполне отчётливо проявившуюся в некоторых случаях. О них далее и пойдёт речь.

Из разборов задач А-26 и А-29 следует, что уравнения {y} – {x} = 0 и sin(πy – πx) = 0 имеют одинаковые графики, то есть – совпадающие множества решений и потому равносильны друг другу:

Согласен, что совпадение множеств решений не так много значит (например, уравнения x² = 0 и ln(x + 1) = 0 тоже имеют одинаковый корень x = 0). Однако выявлены ситуации, когда {x} оказывается увязанным с тригонометрией непосредственно в одном равенстве. Так, в задаче А-33 был построен график функции y = arctg(tg x):

Здесь вполне просматривается похожесть его на график функции дробной части числа, изображение которого на координатной плоскости разбиралось в упражнении А-17:

В комментарии к А-33 был показан график y = arcctg(ctg x), обладающий ещё большим сходством:

Для усиления похожести его несложно модифицировать:

1) «Сжать» график y = arcctg(ctg x) по вертикали (в направлении оси ординат) в π раз:

y1 =

·arcctg(ctg x)

2) «Сжать» по горизонтали (в направлении оси абсцисс), тоже в π раз:

y2 =

·arcctg(ctg(πx))

Получившаяся функция почти полностью совпадает с y = {x} за исключением целых значений аргумента, при которых y₂(x) не определена (на её графике будут «проколы» в этих точках), а функция дробной части равна нулю. Иными словами, если x ∉ ℤ, то выполняется равенство:

{x} = ·arcctg(ctg(πx))

(1)

Данную ситуацию, кстати, легко исправить, доопределив y₂(x) следующим образом:

y3 =

{

0, если x ∈ ℤ y2 = ·arcctg(ctg(πx)), если x ∉ ℤ

Приведённый способ записи с фигурной скобкой вполне общепринят, хотя мне представляется, что в более строгой форме это будет запись в виде объединения двух систем, между которым и выражением функции дробной части числа можно поставить знак равносильности:

⇔   y = {x}

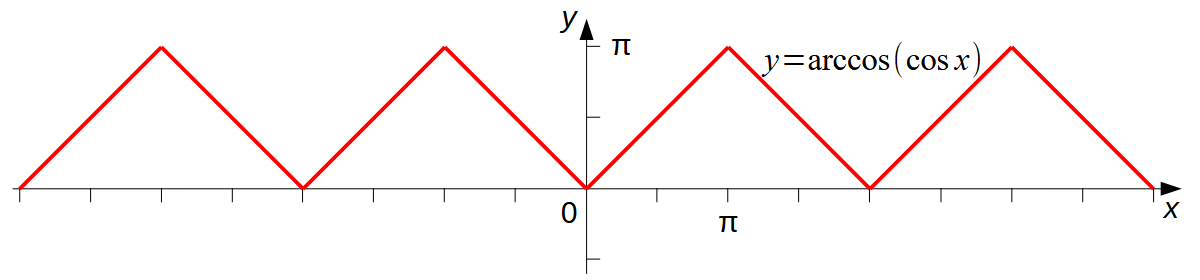
Равенство, когда дробная часть числа выражена через арккотангенс от котангенса справедливо с определёнными оговорками, но мне удалось обнаружить соотношения, такими ограничениями не отягощённые. В задаче А-32 был построен график функции y = arccos(cos x):

Выполним с ним следующие преобразования.

1. «Сожмём» график y = arccos(cos x) по вертикали (вдоль оси ординат) в 2π раз:

y1 =

·arccos(cos x)

2. График y₁ тоже «сожмём» в 2π раз, но уже по горизонтали (вдоль оси абсцисс):

y2 =

·arccos(cos(2πx))

3. «Перевернём» график y₂ умножением на –1:

y3 = –

·arccos(cos(2πx))

4. «Поднимем» график y₃ вверх добавлением к нему половины единицы:

y4 =

–

·arccos(cos(2πx))

В итоге получится ломаная линия, полностью совпадающая с графиком функции y = |{x} – ¹/₂| (см. ответ к задаче А-17):

Выходит, что ∀ x ∈ ℝ имеет место вот такое необычное равенство:

– ·arccos(cos(2πx)) = |{x} – 1/2|

(2)

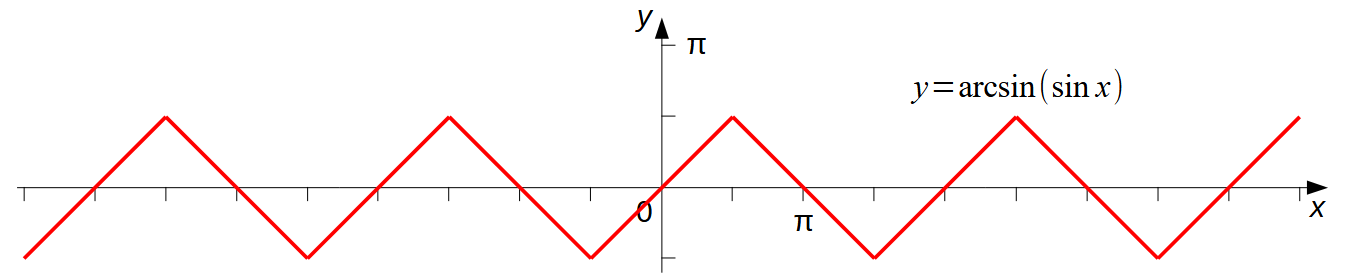
Ещё более мудрёное соотношение можно получить из графика функции arcsin(sin x) (см. упражнение А-31):

1. «Сожмём» график y = arcsin(sin x) в горизонтальном направлении в π раз:

y₁ = arcsin(sin(πx))

2. «Сожмём» график y₁ в вертикальном направлении в π раз:

y2 =

·arcsin(sin(πx))

3. Точки графика y₂ , лежащие ниже оси абсцисс, «отразим» в верхнюю полуплоскость при помощи модуля:

y3 =

·|arcsin(sin(πx))|

4. «Перевернём» график умножением y₃ на –1, а затем то, что получилось, «поднимем» вверх на половину единицы:

y4 =

–

·|arcsin(sin(πx))|

График y₄ полностью совпадает с графиком y = |{x} – ¹/₂|, поэтому можно заключить, что для всех действительных x справедливо выражение:

– ·|arcsin(sin(πx))| = |{x} – 1/2|

(3)

Из одинаковости правых частей (2) и (3) вытекает, что если приравнять левые их части, то после упрощения можно получить ещё одно соотношение (α ∈ ℝ):

arccos(cos 2α) = 2·|arcsin(sin α)|

Затрудняюсь сказать, тянет ли на полноценное строгое доказательство справедливости (1), (2) и (3) факт совпадения графиков функций, но как такое можно выполнить иначе, у меня идей нет, вместо них в наличии лишь сомнения в достаточности собственных знаний по математике для этого.

В заключение заметки стоит вспомнить и об открытости вопроса практической пригодности выведенных формул – подозреваю, что здесь, как и в случае с «параметром круглости», имеет место лишь мозговая гимнастика, обобщающая результаты группы школьных задач.

Добавлено: 29.06.2024

Скачать в pdf