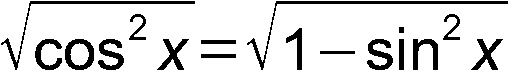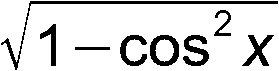В процессе подготовки разборов задач для школьников как-то непроизвольно обращаешь внимание на возможность сделать ряд дополнительных выводов на основании используемых рассуждений, выкладок и результатов. Так было, например, в случае «Размышлений о скругленности и угловатости», затрагивающих группу сходных упражнений по геометрии. Вот и в этот раз оказалось, что из нескольких заданий по алгебре можно вывести ряд своеобразных соотношений.

В задании А-57 выполнялось построение графика функции y = cos(arcsin(sin x)) (рис. 1).

     Рис. 1.

Обращает на себя внимание, что он полностью совпадает с графиком функции y = |cos x|, который можно получить из косинусоиды, если все её точки, лежащие ниже оси абсцисс, зеркально отразить в верхнюю полуплоскость. На основании этого можно записать:

Используя основное тригонометрическое тождество

|cos x| =

и вводя обозначение t = sin x получаем:

Как известно, производная функции арксинус выражается так:

Из соотношения (2) следует, что её можно записать иначе:

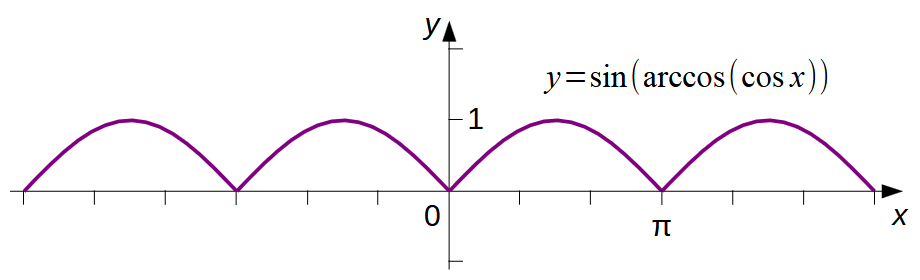
Если теперь обратиться к результату, полученному в задании А-58 (рис. 2), то нетрудно убедиться, что графики y = sin(arccos(cos x)) и y = |sin x| также совпадают, свидетельствуя о справедливости равенства

которое с учётом того, что

|sin x| =

даёт выражение, аналогичное (2):

     Рис. 2.

Трудно не заметить, что одинаковость правых частей (2) и (5) приводит к тождеству, справедливость которого при t ∈ [–1; 1] доказывалось в разборе задания А-56:

Поскольку (arccos x)' = –(arcsin x)' , то соотношение (5) позволяет также записать выражение для производной функции арккосинус в виде

С учётом (6) возможны и такие варианты:

Из рис. 1, 2 видно, что линии графиков обеих функций одинаковы, и один получается из другого смещением на π/2 по оси абсцисс. Из этого следует, что будет выполняться ещё и такое равенство:

cos(arcsin(sin x)) = sin(arccos(cos(x – π/2)))

которое после приведения и замены cos(x – π/2) = sin x = t оказывается тождеством (6).

Добавлено: 23.01.2025

Скачать в pdf