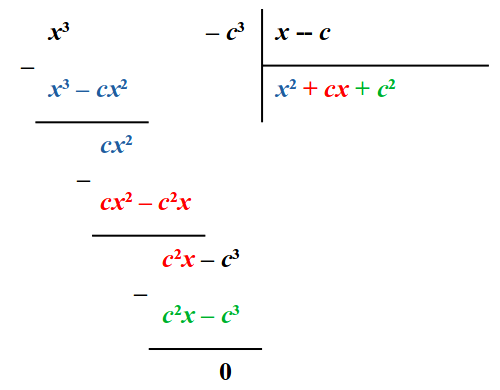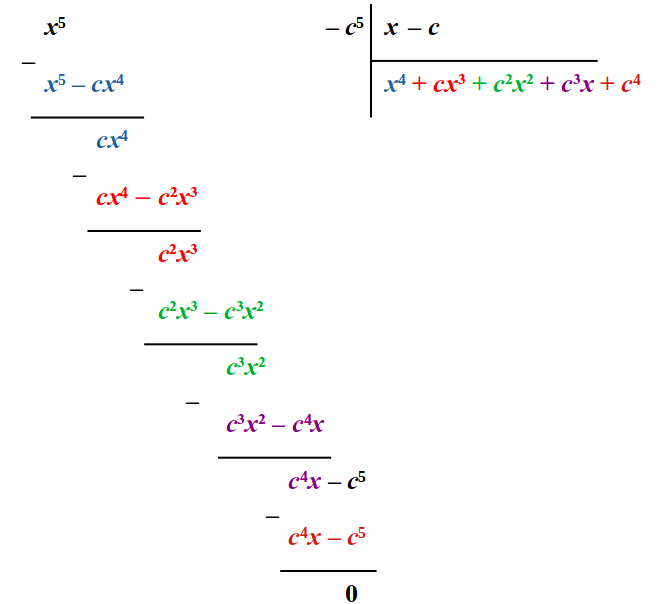На занятиях как в школе, так и в ВУЗе неизбежно к некоторым типам задач испытываешь определённую симпатию, такие задания нравится выполнять. В частности, моё пристрастие к решению химических задач на смешение двух растворов с применением «правила креста» было недавно отмечено одним из комментаторов на дзен-канале. А намного раньше, на уроках алгебры, я особенно предпочитал задачи, в той или иной степени связанные с построением графиков функций. Кстати, освоение такого понятия, как «производная» дало не только комплекс приёмов (нахождение асимптот, нулей функции, областей её возрастания и убывания, точек разрыва и перегиба), расширивший возможности по рисованию графиков, но и породило, если можно так выразиться, «чувство обиды за модуль», ведь при помощи него можно довольно простыми математическими выражениями описывать фигуры весьма затейливой формы (ученики классов с математическим уклоном прекрасно знают, о чём речь), но при этом как в таблице производных, так и в таблице первообразных, функцию y = |x| встретить весьма проблематично, я ведь даже подобную «вопиющую несправедливость» пытался самостоятельно «исправить».

Из того, что меня ещё в своё время удивило, до сих пор памятна такая штука: деление «столбиком» одного многочлена на другой, которое использовалось при решении уравнений высших степеней (мы этим в 10-м классе занимались). Удивление это быстро вылилось в самостоятельный вывод некоторых формул для разложения многочленов на множители. Именно об этом я и хочу рассказать ниже, поскольку почему-то и ныне помню ход своих рассуждений тех времён, а кроме того – подобный материал, как мне кажется, учителями математики вполне может быть использован в качестве задания на занятиях по алгебре.

Стимулом мне тогда послужил простой факт делимости (x³ – 1) на (x – 1), хотя, он весьма тривиален, если помнить соответствующую формулу сокращённого умножения и что 1 = 1³:

x³ – 1³ = (x – 1)·(x² + x·1 + 1²)

Следующим простым и логичным шагом была попытка разделить «столбиком» (то есть так, как совсем недавно научили) многочлен (x³ – c³) на (x – c) (под c подразумевалось постоянное действительное число). И о чудо – частное получилось таким, каким и должно быть, если воспользоваться соответствующей формулой разложения на множители (хотя кто бы сомневался, что могло выйти иначе!):

Аналогичная операция была провёрнута с многочленом (x³ + c³) – он прекрасно поделился на (x + c).

Получив таком образом известные формулы сокращённого умножения для разности и суммы кубов, которые обычно просто даются на уроках «как есть», без вывода, я пошёл дальше и рассмотрел выражение

x⁵ – c⁵

Весьма легко заметить, что оно обращается в ноль при подстановке x = c, то есть уравнение

x⁵ – c⁵ = 0

имеет «лежащий на виду» корень, но это же и означает, что оно представимо в виде

(x – c)·A(x) = 0,

где A(x) – некий многочлен. Отсюда следует, что (x⁵ – c⁵) точно делится на (x – c) и A(x) вполне можно отыскать, используя всё тот же алгоритм деления «столбиком»:

Если теперь равенство

x⁵ – c⁵ = (x – c)·(x⁴ + cx³ + c²x² + c³x + c⁴)

привести к более привычному виду, заменив x на a, а c на b, то получится формула разложения на множители разности двух чисел, возведённых в пятую степень:

a⁵ – b⁵ = (a – b)·(a⁴ + a³b + a²b² + ab³ + b⁴)

Замена x = a, а c = –b даёт ещё одну формулу, на этот раз – разложение на множители суммы двух чисел, возведённых в пятую степень:

a⁵ – (–b)⁵ = (a – (–b))·(a⁴ + (–b)a³ + (–b)²a² + (–b)³a + (–b)⁴) ⇔

⇔ a⁵ + b⁵ = (a + b)·(a⁴ – a³b + a²b² – ab³ + b⁴)

На основании полученных результатов я смог записать эти формулы обобщённо:

a⁵ ± b⁵ = (a ± b)·(a⁴ ∓ a³b + a²b² ∓ ab³ + b⁴)

Затем описанный выше приём был использован для получения и вот такого разложения:

a⁷ ± b⁷ = (a ± b)·(a⁶ ∓ a⁵b + a⁴b² ∓ a³b³ + a²b⁴ ∓ ab⁵ + b⁶)

Ну а далее моё внимание переключилось на какие-то другие вещи (что вполне нормально для пятнадцатилетнего оболтуса) и «копать» глубже в попытках поисках закономерности в полученных формулах я не стал, остановившись на достигнутом.

Не так давно на канале “Valery Volkov” появилось видео, демонстрирующее вывод обобщённой формулы разложения на множители для (aⁿ – bⁿ) – рекомендую к ознакомлению, к тому же именно этот материал заставил вспомнить подробности о своих былых «математических потугах», результаты которых предложены вашему вниманию.

Добавлено: 13.10.2023

Скачать в pdf