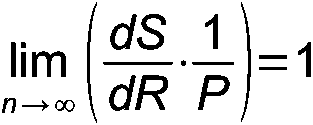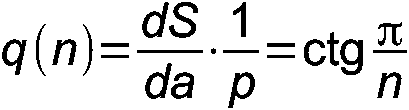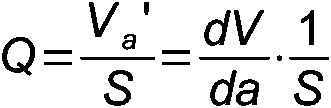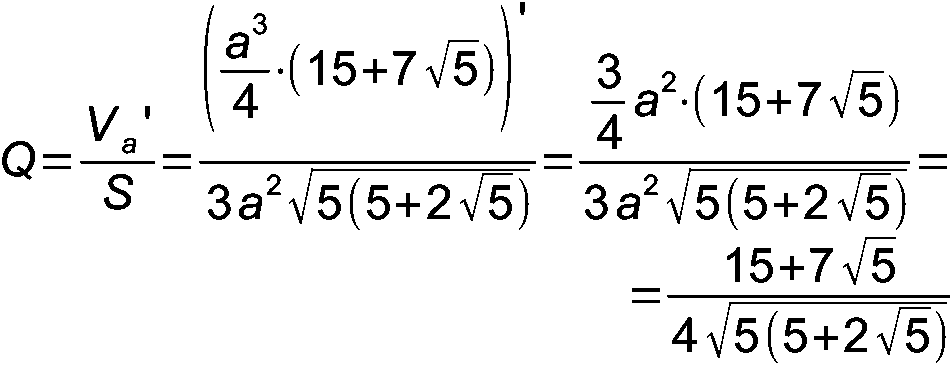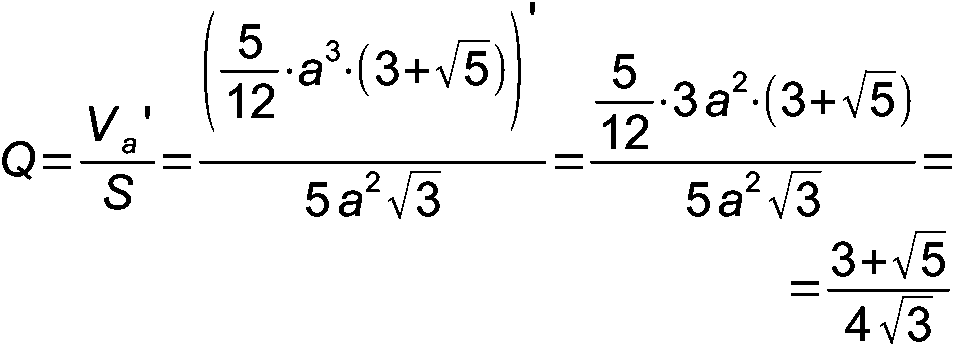Идея написания этой заметки пришла в голову из-за желания сделать некоторое обобщение по ряду публикаций из раздела «Школьные задачи».

В задании Г-10 был рассмотрен правильный n-угольник, вписанный в окружность радиуса R, и было установлено, что при бесконечном возрастании числа сторон отношение производной площади многоугольника по радиусу описанной окружности к периметру этого многоугольника имеет предел, равный единице:

Было также указано, что данное обстоятельство согласуется с тем фактом, что производная площади круга по радиусу есть длина окружности, этот круг ограничивающей. Иными словами, чем больше сторон имеет правильный многоугольник, тем больше он «похож» на окружность. Справедливости ради стоит отметить, что это вполне понятно и на интуитивном уровне, без производных и пределов.

Из решения другой задачи (Г-9), следует, что отношение производной площади правильного многоугольника по его стороне к его же полупериметру есть величина q(n), зависящая только от числа сторон:

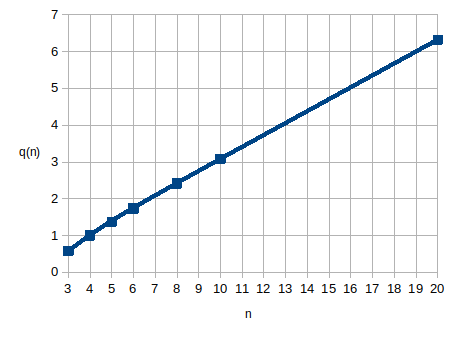
С учётом того, что сторона n-угольника a связана с радиусом описанной окружности R следующим простым соотношением

a = 2R·sin(π/n)

как-то сама собой напрашивается мысль, что q(n) можно рассматривать как своеобразную меру «скругленности» правильного многоугольника – чем этот параметр больше, тем n-угольник «круглее» – ниже это для некоторых значений n демонстрируется на графике.

Производная объёма сферы по радиусу равна площади этой сферы (см. Г-8), а несколько задач (Г-11, Г-12, Г-14) было посвящено нахождению отношения производной объёма V правильного многогранника по стороне его ребра a к его же площади S. По аналогии с правильными n-угольниками возникает мысль попытаться рассмотреть упомянутое отношение в качестве параметра Q, характеризующего меру скругленности многогранника:

Правильных многогранников (т. н. «платоновых тел») известно пять, в задачах величина Q была определена для тетраэдра (Г-12), куба (Г-11) и октаэдра (Г-14). За сведениями об остальных многогранниках проще всего залезть в математический справочник.

Для додекаэдра [1, с. 49] получаем:

В случае икосаэдра:

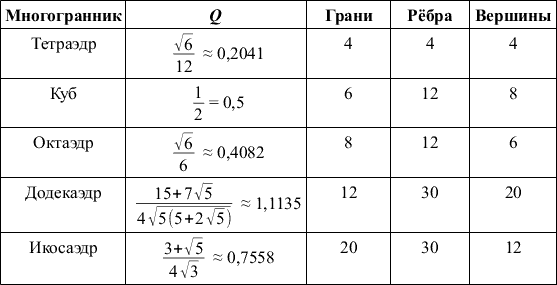
Для удобства данные лучше свести в таблицу:

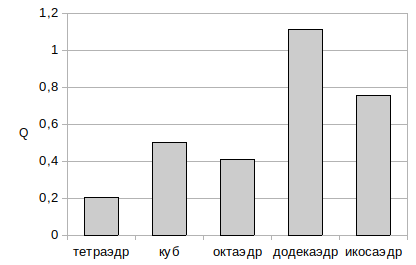
Если изобразить значения Q для многогранников в виде гистограммы, получится вот это:

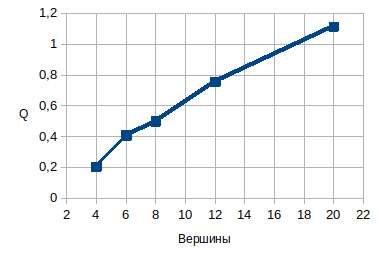
Так как полученные в случае многоугольников значения q(n) возрастают при увеличении n, то возникает желание каким-то образом упорядочить и Q на основании какого-либо количественного свойства многогранника. В таблице выше приведены числа граней, рёбер и вершин. Оказывается, что Q монотонно увеличивается при возрастании количества вершин у многогранника:

В целом выходит, что если отталкиваться от значения Q, то додекаэдр получается наиболее округлым многогранником, а тетраэдр наоборот – самым угловатым.

Вот такие вот своеобразные размышлялки под самый Новый год получились… Самое забавное, что как и в случае с когда-то придуманной мной же «арифией» непонятно, где эти результаты мозговой гимнастики на геометрическую тему можно использовать, ведь единственное, что всплывает в памяти о практическом применении предметов в форме правильных многогранников – специальные игральные кости («дайсы»). Например, в комплекте с изданной в 1992 г. книгой-игрой «Кощеева цепь» (автор – Шувалов В.) шла специальная восьмигранная кость, стороны которой располагались соответственно граням правильного октаэдра.

Литература:

[1]. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). М.: Наука, 1974. – 832 с.

Добавлено: 27.12.2023

Скачать в pdf