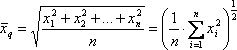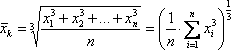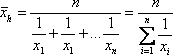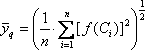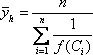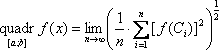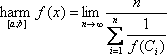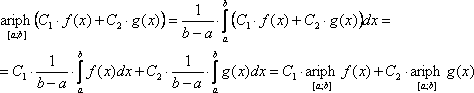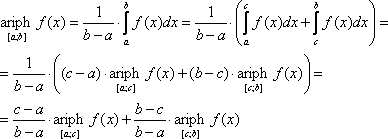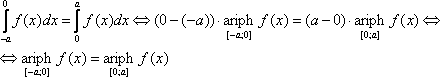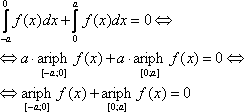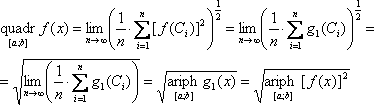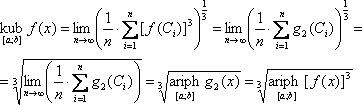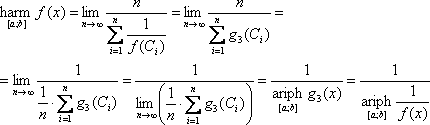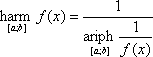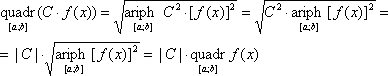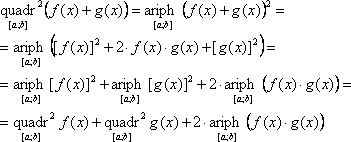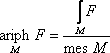Жизнь у всех разная и проявляется это ещё и в том, что источники информации, с которыми мы имеем дело, тоже у всех различны. Кроме этого, далеко не каждые сведения оставляют нас равнодушными, не вызывая совершенно никаких эмоций или мыслей. При этом иногда сочетание данных из двух источников может побуждать к весьма своеобразным умозаключениям.

Есть у меня одна книга – пособие для учителя информатики ^[1]. Не помню, как она у меня появилась – может купил, а может мне её кто-то подарил – однако в школе она мне как-то пригодилась в освоении языка Basic, программы на котором мы тогда собственноручно набивали на болгарских машинах «Правец 8A». Именно из этой книги я когда-то впервые узнал, что помимо так называемого среднего арифметического для нескольких чисел бывает, например, ещё и среднее квадратическое.

На первом курсе (1999-2000 гг.) университета, на лекциях по высшей математике, когда мы проходили определённые интегралы, была упомянута так называемая «теорема о среднем» ^{[2, с. 353]}. И вот это-то, в комбинации с сидящими в памяти сведениями из упомянутой книги, почему-то отозвалось в мозгах вопросом: «А какое именно среднее имеется в виду в теореме: арифметическое, кубическое или какое-нибудь другое?». Ну а раз возник вопрос – можно попытаться найти и ответ. Поиск сей вскоре привёл меня к тому, что, собственно, и составляет основу материала данной заметки. Свои измышления я условно назвал «теорией средних» и достаточно долгое время они хранились у меня в виде конспекта. Теперь же результаты этой «мозговой гимнастики» я выложил в сеть по следующим соображениям. Во-первых, если на этот материал наткнётся математик, то, думается, это сможет его повеселить. Во-вторых, мне слабо верится, что никто из профессиональных математиков в своих работах не додумался до чего-то подобному тому, что изложено здесь. В связи с этим мне особенно интересно было бы узнать, чьи это результаты мной, вероятно, «переоткрыты» – к сожалению, я не располагаю возможностью и временем это выяснить самостоятельно, но буду очень благодарен за сведения об этом.

I. Типы средних (введение)

Пусть у нас имеется множество из n чисел x₁, x₂,...x_n.

а) Среднее арифметическое этих чисел:

б) Среднее квадратическое:

в) Среднее кубическое:

г) Если ни одно из чисел рассматриваемого множества не равно нулю, то для них можно вычислить среднее гармоническое ^{[1, с. 132]}:

II. Средние значения функции на замкнутом числовом промежутке

Рассмотрим непрерывную функцию y=f(x), определённую на отрезке [a; b]. Разобьём [a; b] на n равных частей величиной Δx_i=(b–a)/n. Теперь внутри каждого отрезка разбиения Δx_i произвольно выберем точку C_i () и вычислим значение функции y=f(x) в точке C_i: y_i=f(C_i) (Рисунок 1).

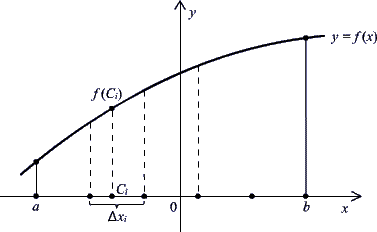
Рисунок 1.

Для полученного таким образом множества значений по формулам (1), (2), (3) можно вычислить средние арифметическое, квадратическое и кубическое:

В случае, если f(x) на [a; b] ни в одной точке не обращается в ноль, то по (4) можно вычислить и среднее гармоническое:

Будем теперь увеличивать неограниченно n и найдём пределы выражений (5), (6), (7) и (8) при n→∞. Если эти пределы существуют для рассматриваемой функции y=f(x) на отрезке [a; b], то назовём их, соответственно, средним арифметическим, средним квадратическим, средним кубическим и средним гармоническим значениями функции y=f(x) на отрезке [a; b]. Введём обозначения:

Для удобства операторы

, , ,

назовём арифией, квадрией, кубинией и гармонией соответственно.

III. Вычисление арифии функции на замкнутом числовом промежутке

Вернёмся к Рисунку 1. Составим для функции f(x) интегральную сумму Римана:

Эта сумма при неограниченном возрастании n имеет предел, равный интегралу:

Величина (b – a) – длина отрезка [a; b] – число постоянное, поэтому

Подставим (9) в (13):

или

Из (14) как раз и следует ответ на возникший у меня вопрос: в теореме о среднем фигурирует именно среднее арифметическое значение функции на отрезке (придуманная мной "арифия").

IV. Свойства арифии функции на отрезке

Свойство 1 (свойство линейности оператора арифии):

(C₁ и C₂ – постоянные числа, f(x) и g(x) – непрерывные и определённые на [a; b] функции).

Доказательство:

Свойство 2. Если C=const, то

Доказательство:

Свойство 3. Если a < c < b, то

Доказательство:

Свойство 4. Если f(x) – чётная функция и a > 0, то

Доказательство:

Так как f(x) – чётная, то

Далее:

,   .

Отсюда:

Свойство 5. Если f(x) – нечётная функция, то

Доказательство:

Так как f(x) – нечётная, то

,

отсюда

Свойство 6.

Доказательство:

Известно, что

Домножим обе части этого неравенства на (b – a) (b – a > 0):

V. Вычисление квадрии, кубинии и гармонии функции на отрезке

Пусть g₁(x)=[f(x)]², тогда

Итак:

Пусть теперь g₂(x)=[f(x)]³, тогда

или

Пусть теперь функция y=f(x) на [a; b] ни в одной точке не принимает нулевого значения. Обозначим .

Окончательно:

VI. Свойства квадрии, кубинии и гармонии функции на отрезке

Свойство 7. Если C=const:

Доказательство:

Свойство 8.

Доказательство:

Аналогично доказываются следующие соотношения:

и (если C ≠ 0)

Свойство 9.

Доказательство:

Свойство 10.

Доказательство:

Из (22):

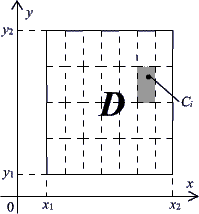
VII. Среднее значение функции нескольких переменных

По аналогии со средним значением функции на замкнутом числовом промежутке можно рассмотреть вопрос о среднем значении функции нескольких переменных в некоторой области значений её аргументов. Рассмотрим это на примере непрерывной функции двух независимых переменных z=f(x, y), определённой в некоторой области прямоугольной формы D. Разобьём эту область на k=n·m (n, m – целые числа) одинаковых площадок, внутри каждой из них произвольно выберем точку C_i () и вычислим значение функции z_i в каждой из них (Рисунок 2).

Рисунок 2.

Далее, по аналогии с (5) можно вычислить среднее полученных значений функции (например, среднее арифметическое):

Теперь можно начать неограниченно увеличивать n и m (и, соответственно, k) и найти предел выражения (33) при n → ∞, m → ∞ (k → ∞). Если этот предел существует для рассматриваемой функции, то его можно назвать средним арифметическим значением функции f(x, y) в области D. По аналогии с (9) можно ввести обозначение:

В соответствии с Рисунком 2 площадь каждого из k участков разбиения области D равна (S_D – площадь области D):

Составим для функции f(x, y) интегральную сумму Римана:

Эта сумма при неограниченном возрастании k имеет предел, равный следующему интегралу:

Так как S_D – число постоянное, то

Из полученного равенства следует формула для вычисления арифии функции двух переменных в области D:

Используя похожие рассуждения, можно также ввести определения для квадрии, кубинии и гармонии и получить формулы для их вычисления. Например:

Для функции трёх переменных t=f(x, y, z) формула для вычисления арифии в области v, имеющей форму прямоугольного параллелепипеда объёмом V_v, выглядит следующим образом:

При желании можно исследовать и свойства таких «средних». Так, оператор арифии обладает свойством линейности для функций одного, двух и трёх независимых переменных. Кроме этого, нетрудно заметить, что арифия во всех рассматриваемых случаях вычисляется сходным образом. Это позволяет написать условную обобщённую формулу для её вычисления: если мы имеем некоторую функцию F, то её среднее арифметическое значение в некоторой области M будет равно частному соответствующего интеграла функции по этой области и меры области (длины, площади или объёма):

В той книге по информатике была приведена ещё одна формула для среднего геометрического, определявшегося как корень степени n из произведения n чисел (надо полагать, неотрицательных). В принципе, ничто не мешает (с соответствующими оговорками и ограничениями) придумать «среднее геометрическое значение функции» и способ его вычисления (оно через логарифмирование фактически сводится к вычислению арифии логарифма исходной функции).

Литература:

[1]. Касаткин В.Н. Информация, алгоритмы, ЭВМ: Пособие для учителя. – М.: Просвещение, 1991. – 192 с.: ил.

[2]. Пискунов Н.С. Дифференциальное и интегральное исчисления. Учеб.: в 2-х т. Т. 1 – СПб.: Мифрил. Гл. ред. Физ.-мат. лит., 1996. – 416 с.

Добавлено: 02.10.2011

Изменено: 02.10.2011

Скачать в pdf