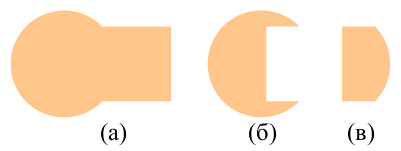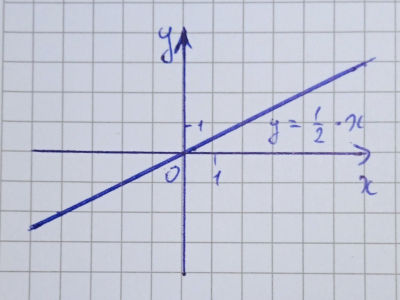
Иногда для некоторых заметок на сайте пишутся продолжающие их дополнения. В этот раз долго не получалось решить, где разместить материал, которой будет предложен далее вашему вниманию – он вполне подходит как для публикации «Школьные задачи», так и для «Мои сайт и дзен-канал: как это делается». В итоге я счёл, что рациональнее оформить его в виде отдельной заметки, посвящённой одной любопытной возможности приложения LibreOffice Draw.

Помимо знаний от уроков математики у меня остались убеждения о том, каков «канонический» вид рисунка декартовой системы координат, в области которой изображаются графики функций и прочие объекты типа векторов и т. п.:

• положительное направление координатных осей обозначается «стрелочками» на концах;
• оси подписываются символами переменных, значения которых по ним откладываются;
• начало координат обозначается символом нуля;
• на осях указывается их масштаб соответствующими отметками (обычно это единичный отрезок, но можно и иной, если в конкретном случае это более уместно, например π или e);
• объекты на координатной плоскости подписываются (например, график функции – её математическим выражением).

«Школьные задачи» постепенно «выросли» из скромной заметки в самостоятельный раздел на сайте, и из-за специфики иллюстраций, необходимых для оформления публикуемых задач и их решений, возникла регулярная потребность рисовать графики функций. Разумеется хотелось, чтобы и выглядело это всё максимально соответствующим привитым ещё в школе правилам. Такое желание привело к разнообразному экспериментированию с картинками – в этом можно легко убедиться, если просмотреть публикации с разбором упражнений по алгебре.

Касаемо самого характера рисунков довольно логичным является стремление использовать векторные изображения ввиду их лучшей пригодности для данных целей. И вот, казалось бы – бери программу для работы с электронными таблицами и вперёд – там есть инструменты для построения диаграмм, которые суть векторные картинки. Возможности штатных средств в популярных табличных процессорах (Microsoft Excel и LibreOffice Calc) действительно весьма неплохи, но, как оказалось, всё равно недостаточны для реализации моих «хотелок». В частности, в Calc я не нашёл такой, казалось бы, элементарной вещи, как «стрелочки» на концах координатных осей (при этом в настройках диаграммы в Excel эта возможность есть).

В такой ситуации вполне нормальным шагом было взять и нарисовать в Draw то, что мне нужно, и так, как мне нужно. Такой подход в целом неплохо работает, например:

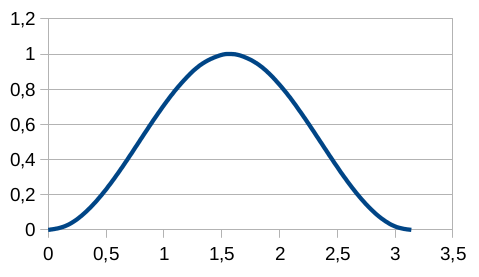
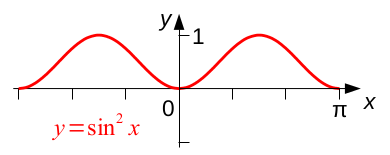
Сложности начинаются при попытке изобразить что-нибудь «непрямое» поточнее – хотя бы банальную квадратичную параболу. Именно это обстоятельство довольно долго ограничивало использование Draw, но недавно у меня получилось самостоятельно «нащупать» способ, которым мне хотелось бы поделиться – может, он кому-нибудь тоже пригодится (описание дальнейших действий приводится для приложений пакета LibreOffice версии 7.6.6).

1.1) Создаём в Calc диаграмму с нужным нам изображением. Для примера построен график функции y = sin²x в диапазоне значений аргумента [0; π] (точнее – в диапазоне от 0 до 3,14159), тип диаграммы «XY разброс», вариант «Только линии», тип линии «Сглаженная»:

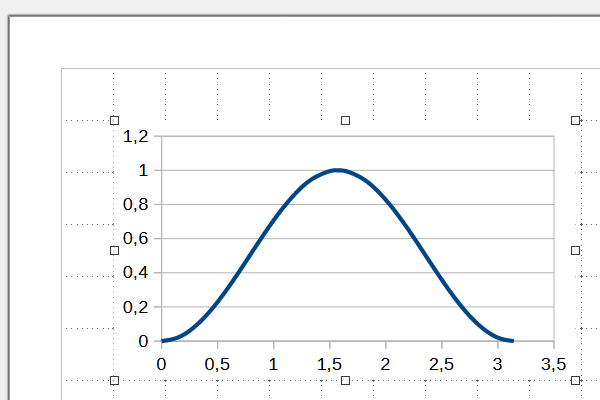
1.2) Выделяем эту диаграмму, копируем её в буфер обмена и вставляем в новый файл (рисунок) Draw. Благодаря тому, что это приложение входит в тот же самый программный пакет, подобный обмен происходит адекватно, без неприятных сюрпризов.

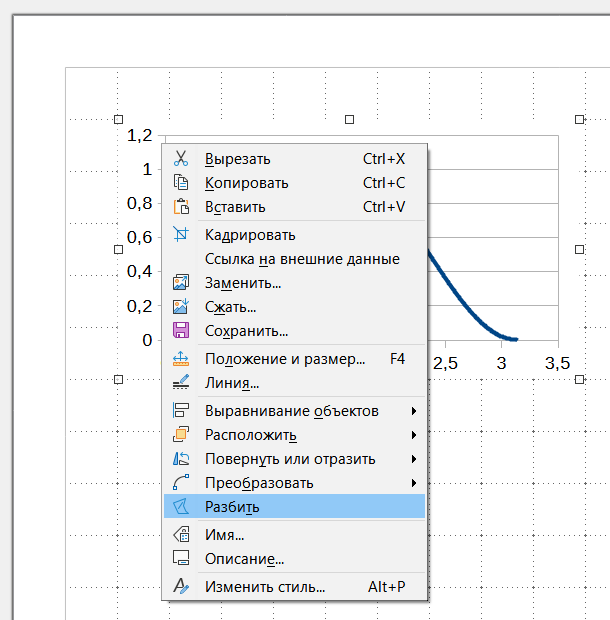
1.3) Щелчком правой кнопкой мыши по диаграмме вызываем контекстное меню и выбираем в нём команду «Преобразовать» → «В метафайл»:

1.4) Делаем ещё один правый щелчок и в новом контекстном меню выбираем команду «Разбить»:

1.5) Диаграмма «разваливается» на отдельные элементы, среди которых будет и собственно кривая графика функции (фрагмент синусоиды). Не знаю почему, но часть элементов «разбитой» диаграммы самопроизвольно «отскакивает» в сторону верхнего левого угла изображения – вероятно, это какой-то программный «баг», который разработчики со временем, надеюсь, «пофиксят».

1.6) Нужный элемент (фрагмент синусоиды) можно скопировать отдельно и отмасштабировать необходимым образом:

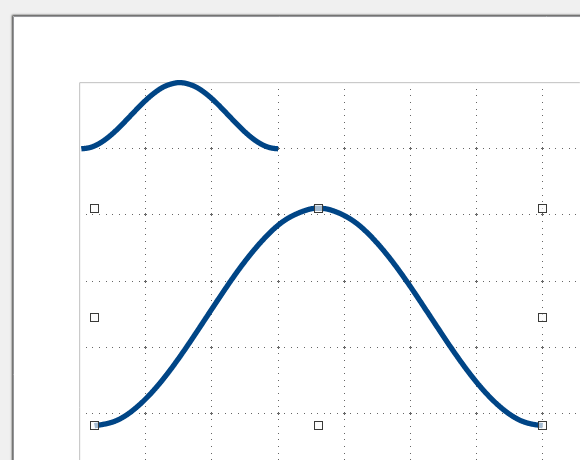
Линию графика функции можно модифицировать не только меняя её габариты, но и, например, настроить по своему вкусу толщину и цвет и использовать далее для компоновки нужного рисунка:

Вид такой иллюстрации вполне соответствует моим предпочтениям, тем не менее даже описанного приёма не всегда оказывается достаточно. Иногда возникает необходимость нарисовать некоторую область сложной формы – например, в случаях задач по изображению множества точек, координаты которых удовлетворяют некому условию (или набору условий). Рассмотрим, как это делается на примере линии синусоиды – превратим её в соответствующую область с заливкой.

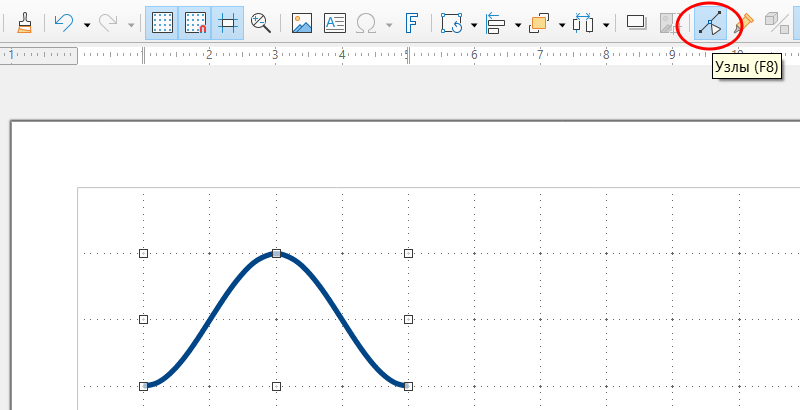
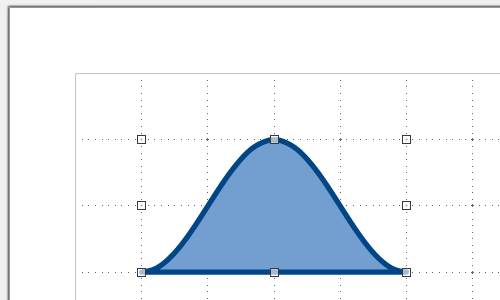
2.1) Выделяем линию и на панели инструментов нажимаем кнопку «Узлы»:

На кривой отобразятся маркеры узловых точек, по которым она и построена. Поскольку их довольно много, то в данном случае они полностью закроют собой саму линию:

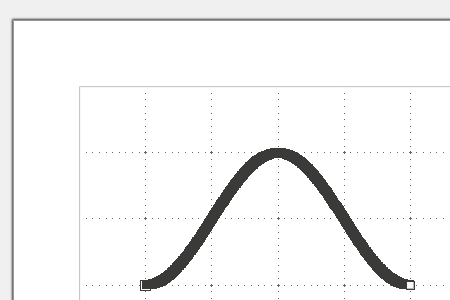
2.2) На появившейся вспомогательной панели инструментов нажимаем кнопку «Замкнуть кривую Безье». Начальный и конечный узлы соединятся отрезком и образуется замкнутая фигура, которой автоматически сообщается заливка.

Если отключить показ узловых точек (отжатием кнопки «Узлы»), то фигура будет иметь такой вид:

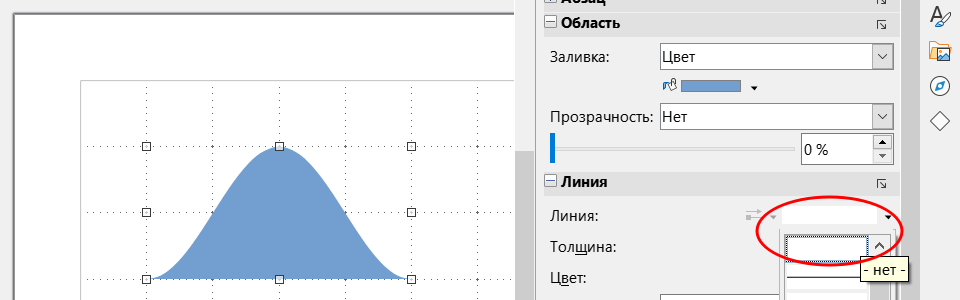
2.3) Для дальнейших операций с такой областью контур обычно бывает лишним, поэтому его лучше отключить, выбрав в настройках объекта отсутствие линий:

Полученный объект также можно дополнительно настраивать, например, регулировка прозрачности хорошо подходит для наглядного показа пересекающихся множеств. На рисунке ниже точки, координаты которых удовлетворяют неравенству y ≥ –(sin²x + 1), образуют область с синей заливкой, а множество точек, соответствующее неравенству y < 0 – зону жёлтого цвета. Так как визуально при смешении синего с жёлтым получается зелёный, пересечение множеств, то есть решение системы из двух рассматриваемых неравенств, выглядит как зелёная область:

Кстати, для изображения областей нужной формы был использован имеющийся в арсенале Draw приём – «алгебра» векторных объектов. Что это такое, лучше показать на конкретном примере. Рассмотрим две пересекающиеся геометрические фигуры:

Если их обе выделить (щёлкнуть мышью по одной, а затем, зажав клавишу [Shift], щёлкнуть по другой) и вызвать контекстное меню щелчком правой кнопкой мыши, то там будет пункт «Фигуры», который раскрывается в новое подменю. В нём нас интересуют команды сложить, вычесть и пересечь:

Работают они так. При сложении фигуры-операнды просто сливаются в одну с общим для них обеих контуром (а). При вычитании из фигуры на заднем плане (в данном случае это круг) отнимаются точки, общие с фигурой на переднем плане (б). Результат пересечения вполне говорит сам за себя – это фигура, содержащая совместные точки обоих операндов (в):

Описанный приём позволяет на основе фигур, подобных полученной в пп. 2.1)-2.3), создавать довольно сложные по форме области.

Вот так вот не нарочно получился миниатюрный ликбез по работе с редакторами векторной графики, потому что подобные приёмы можно встретить и в других программах такого типа. Кроме этого, найденная возможность добиться от Draw того, что мне нужно, позволяет реализовать ещё одну свою задумку – наконец-то оформить упражнения раздела «Школьные задачи» в виде отдельного сборника, доступного для скачивания. Помимо заданий, разбор решения которых опубликован на сайте и дзен-канале, туда вошли дополнительные упражнения, кроме этого, я по возможности постарался подчеркнуть наличие у задач междисциплинарных связей.

Добавлено: 15.05.2024

Скачать в pdf