|
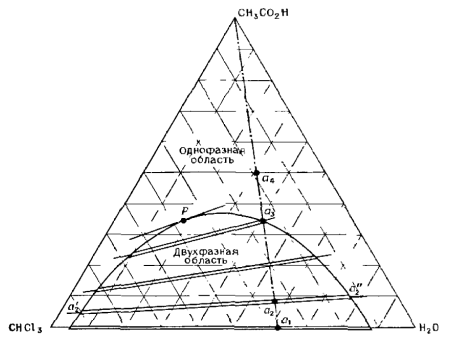
На третьем курсе на занятиях по физической химии мы изучали различные диаграммы состояния. Особо запомнились своим довольно необычным видом такие диаграммы при постоянных температуре и давлении для систем, состоящих из трёх веществ, так как изображались они в виде равностороннего треугольника (т. н. «треугольник Гиббса-Розебома»), где каждая его точка соответствовала смеси какого-либо определённого состава (рис. 1, 2), а концентрации выражались как доли компонентов.
Рис. 1. Трёхкомпонентная система уксусная кислота – хлороформ – вода при комнатной температуре [1, с. 338].
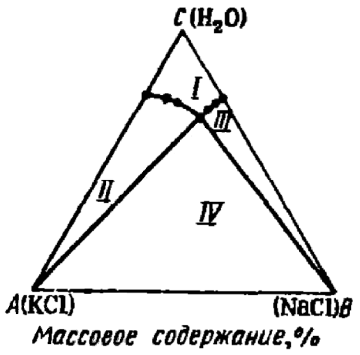
Рис. 2. Диаграмма растворимости KCl и NaCl в воде при 298 К [2, с. 485]. Также на лекциях нам рассказывали про два правила, по одному из которых каждой точке треугольника-диаграммы ставился в соответствие состав трёхкомпонентной смеси. Опишу кратко эти правила [3, с. 229] на примере системы из веществ A, B и C, мольные доли которых составляют x, y и z соответственно. Рассмотрим точку D внутри равностороннего треугольника △ABC (рис. 3). Какому соотношению x : y : z она соответствует?
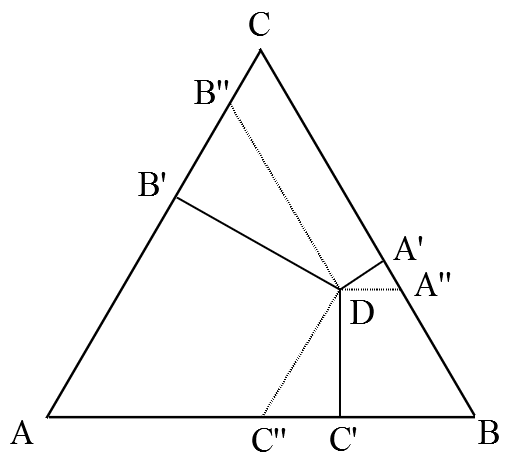
Рис. 3. Определение состава смеси по правилам Гиббса и Розебома. 1) По правилу Гиббса высота треугольника принимается за единицу (или за 100%) и используется тот факт, что сумма длин перпендикуляров, опущенных из точки D на стороны треугольника равна его высоте. В этом случае концентрации (доли) компонентов пропорциональны длинам этих перпендикуляров: x : y : z = DA' : DB' : DC' или
2) По правилу Розебома за единицу (за 100%) принимается длина стороны треугольника, при этом из точки D проводятся отрезки, параллельные каждой из его сторон (на рис. 3 это DA'', DB'', DC''). Сумма их длин равна стороне треугольника и выполняется следующее соотношение: x : y : z = DA'' : DB'' : DC'' или в иной записи
Легко видеть, что правила Гиббса и Розебома нисколько не противоречат друг другу: x : y : z = DA' : DB' : DC' = DA'' : DB'' : DC'' Это обусловлено тем, что △DA'A'', △DB'B'' и △DC'C'' являются подобными (как треугольники с равными углами: ∠DA'A'' = ∠DB'B'' = ∠DC'C'' = 90°; а ∠DA''A' = ∠DB''B' = ∠DC''C' = 60°, поскольку DA'' || AB, DB'' || BC, DC'' || AC). Простого запоминания описанных правил вполне хватило для подготовки к сдаче экзамена, тем более дальнейшая жизнь сложилась так, что за все последующие годы с диаграммами состояния мне иметь дело особо-то и не доводилось. Тем не менее в те времена появилось ощущение, что что-то в этих правилах определения состава системы меня смущает и спустя год я понял, что же именно. Дело было в следующем. Очевидно, что доли компонентов системы связаны между собой соотношением
однако из такого равенства неизбежно следует, что для графического изображения множества точек, координаты которых удовлетворяют такому равенству, необходимо использовать трёхмерное пространство, потому что переменных в уравнении три, но при этом треугольник Гиббса-Розебома – это именно треугольник, то есть плоская (двумерная) фигура. Почему так? В итоге до меня дошла очень простая вещь: если переписать (3) как
то получается известное из аналитической геометрии «уравнение плоскости в отрезках», которое в общем виде записывается так:
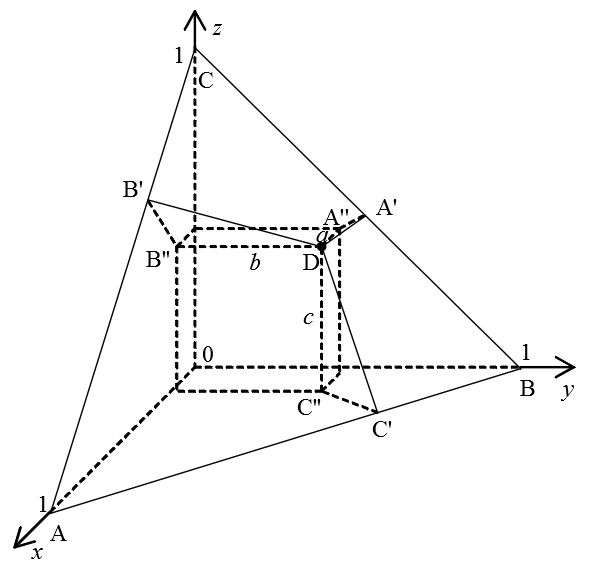
где l, m и n – точки, в которых данная плоскость пересекает оси абсцисс, ординат и аппликат соответственно. Отсюда получается, что треугольник Гиббса-Розебома располагается именно в плоскости, описываемой уравнением (4). Можно сказать иначе: поскольку каждая из величин x, y, z принимает значения от 0 до 1 (потому что это доли компонентов в смеси), то треугольник Гиббса-Розебома является расположенным в первом октанте графиком функции z = 1 – x – y Из этого факта как раз и следует, что для построения диаграммы состояния трёхкомпонентной системы вполне достаточно плоского изображения. А ещё любопытно здесь другое. Взгляните на рис. 4 – на нём изображён треугольник Гиббса-Розебома в «трёхмерном» представлении.
Рис. 4. Треугольник Гиббса-Розебома, представленный как график функции z = 1 – x – y . В △ABC выбрана точка D, от которой к сторонам этого треугольника проведены перпендикуляры DA', DB', DC'. Сама точка D имеет координаты (a, b, c), численные значения которых являются концентрациями входящих в состав смеси компонентов. Вершины △ABC с точкой начала координат образуют тетраэдр и из симметрии данного геометрического тела следует, что двугранные углы, образованные плоскостью △ABC и координатными плоскостями, равны. При этом в соответствии с теоремой, обратной теореме о трёх перпендикулярах
В связи с этим мне в голову уже давно закралась следующая мысль: а может создатели диаграмм состояния, когда разрабатывали способы наглядного преставления характеристик трёхкомпонентых систем, руководствовались схожими соображениями – про уравнение плоскости «в отрезках», про получающиеся при этом подобные треугольники и т. д.? Не удивлюсь, если такое действительно было опубликовано тем же самым Дж.У. Гиббсом в своих научных работах, а теперь, спустя более века и став классикой, успело подзабыться. В учебниках по физической химии, на которые я выше ссылался, и в ряде других [5, с. 422; Кстати, схожая ситуация наблюдается и в отношении «правила креста» – очень легко отыскать литературу и сайты, где подробно рассказывается как решать задачи на смешение растворов с использованием этого правила, а вот материала, в котором описано откуда именно это правило берётся (то есть его математическое обоснование), мне обнаружить не удалось – пришлось восполнять этот пробел самостоятельно написанием соответствующей заметки. Литература:
Добавлено: 20.03.2021 Изменено: 20.03.2021 |