◁◁◁

Тематические серии:

• задачи на построение: Г-2, Г-6, Г-7
• соотношение между длиной и производной площади: Г-13, Г-8, Г-9, Г-10
• соотношение между площадью и производной объёма: Г-8, Г-11, Г-14, Г-18
• сумма частных производных: Г-13, Г-18
• нахождение векторов, угол между которыми задан: Г-15, Г-16, Г-17
• разные задачи: Г-1, Г-4, Г-5, Г-3

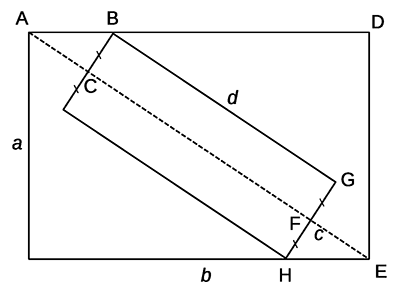
Г-1. Доказать, что сумма синусов углов треугольника равна отношению периметра треугольника к диаметру описанной вокруг него окружности.

Г-2. Дано два равносторонних треугольника. При помощи циркуля и линейки построить третий равносторонний треугольник, площадь которого равна сумме площадей первых двух.

Г-3. Тетраэдр, у которого все рёбра имеют одинаковую длину, называется правильным, и он обладает следующими свойствами: а) все четыре грани тетраэдра являются равносторонними треугольниками, равными между собой; б) любая его высота пересекает грань в точке, равноудалённой от каждого из рёбер этой грани; в) внутри тетраэдра есть точка, которая равноудалена от его вершин и является точкой пересечения высот тетраэдра.

Найти косинус угла, вершина которого находится в точке пересечения высот тетраэдра, а стороны проходят через любые две его вершины.

Г-4. Попавший ночью в шторм парусник затонул. Из экипажа выжить удалось лишь одному человеку, который остался на поверхности воды и держится за спасательный круг. На рассвете небо полностью расчистилось от облаков и наступил полный штиль. В 15 км от выжившего оказался ещё один парусный корабль, на мачте которого в «вороньем гнезде» дежурит очень зоркий матрос и с высоты 15 м над водой осматривает море окрест. Сможет ли он увидеть выжившего в кораблекрушении, чтобы сообщить капитану судна о человеке за бортом?

При решении задачи рекомендуется использовать инженерный микрокалькулятор; радиус Земли считать равным 6370 км.

Г-5. Внутри прямоугольника со сторонами a и b расположен ещё один прямоугольник со сторонами c и d так, как показано на рисунке – одна из диагоналей внешнего проходит через середины сторон внутреннего и две вершины внутреннего лежат на сторонах внешнего. Считая величины a, b и c известными, найти значение d.

Г-6. Даны два отрезка с длинами а и а (a – неотрицательное действительное, n – натуральное). При помощи циркуля и линейки построить отрезок с длиной а.

Г-7. Даны два отрезка с длинами а и а (a – неотрицательное действительное; n – натуральное, равное или большее двух). При помощи циркуля и линейки построить отрезок с длиной а.

Г-8. Дана сфера с радиусом R. Доказать, что: а) первая производная объёма сферы по радиусу равна её площади; б) вторая производная объёма сферы по радиусу равна учетверённой длине её большой окружности.

Г-9. Длина стороны правильного многоугольника равна a. Найти производную его площади по стороне.

Г-10. Вокруг правильного многоугольника с числом сторон n описана окружность радиусом R. Найти предел отношения производной площади многоугольника S по радиусу R описанной окружности к периметру P этого многоугольника при бесконечном увеличении n:

Г-11. Чему равно отношение производной объёма куба по стороне к площади его поверхности?

Г-12. Дан правильный тетраэдр с ребром, равным a. Найти отношение производной его объёма по длине ребра к площади поверхности.

Г-13. Доказать, что сумма частных производных площади прямоугольника по его сторонам равна полупериметру этой фигуры.

Г-14. Для правильного октаэдра с длиной ребра a найти отношение производной его объёма по ребру к площади поверхности.

Г-15. На плоскости дано два ненулевых вектора с координатами (c; c²) и (c; c³). Найти все действительные значения c, при которых векторы будут взаимно перпендикулярны.

Г-16. В трёхмерном пространстве заданы два ненулевых вектора с координатами (–2c; c; c) и (c; c²; c³). Найти все действительные значения c, при которых векторы будут взаимно перпендикулярны.

Г-17. На плоскости дано два ненулевых вектора с координатами (c; c) и (c; c²). Найти все действительные значения c, при которых угол между векторами будет равен 60°.

Г-18. Доказать, что сумма частных производных объёма прямоугольного параллелепипеда по сторонам равна половине площади его поверхности.

Добавлено: 14.08.2019

Изменено: 19.03.2024