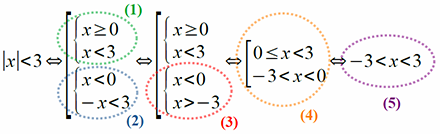В начале публикации «Учим символы химических элементов» я упоминал, что наукам присущи особые системы условных обозначений. Разумеется, это относится и к математике тоже. И хотя я выпускник химического факультета, ниже мне придётся, действуя из хороших побуждений, позволить себе наглость залезть в «чужой математический огород» и вот почему.

Заметка «Школьные задачи» в разделе сайта «Соображалки», впервые выложенная в Сеть ещё в 2007 году, постепенно начала разрастаться из-за новых добавляемых в неё заданий. Недавно я счёл более целесообразным вернуть её в состояние, близкое к исходному, параллельно организовав в разделе «Самоделки» новый подраздел, одноимённый с указанной заметкой. У некоторых задач по алгебре способ записи приведённого там хода решения знаком далеко не всем школьникам, в связи с чем написанное далее посвящено разъяснению используемой символики на примере построения графика вот такой функции:

y = | |x| – 1 |

Начну я свой рассказ с того, что у математиков есть специальный знак, заменяющий слово «равносильно»:

⇔

Например, чтобы показать, что равенство

x + 1 = 3

ничем по сути не отличается от равенства

x = 2

пишут:

x + 1 = 3 ⇔ x = 2

Помимо краткости – вместо целого слова ставится лишь один символ – удобство здесь заключается и в том, что подобные обозначения являются интернациональными, то есть приведённую запись одинаково поймут и математик из Мексики, и математик из Франции, несмотря на то, что её написал кто-то из России, не знающий ни испанского, ни французского языков.

Ещё в арсенале средств математической науки есть набор разномастных скобок, из которых нам в данный момент будут интересны открывающая фигурная:

{

и открывающая квадратная:

[

Первая используется для обозначения «связки» нескольких математических выражений с целью показать требование одновременного выполнения их всех, то есть фигурная скобка как бы соединяет математические «фразы» союзом «И». Думаю, нет нужды напоминать, что именно так записываются, например, системы алгебраических уравнений, типа таких:

Смысл этой записи можно трактовать следующим образом: «Предполагается существование таких двух чисел x и y, которые при подстановке обращают выражение x + y = 7 И выражение x – 2y = 1 в верные числовые равенства».

Квадратная открывающая скобка обозначает объединение – связывание ряда математических «высказываний» с требованием выполнения хотя бы одного из них. Иначе говоря, она работает подобно союзу «ИЛИ». Если, допустим, некое квадратное уравнение имеет два корня x₁ = 1, x₂ = 3, то это можно записать и так:

Подобную конструкцию можно понимать как утверждение: «При подстановке в уравнение вместо переменной числа 1 ИЛИ числа 3 оно обращается в верное числовое равенство».

Перед тем, как переходить к построению графика, давайте рассмотрим решение вот такого простого неравенства:

|x| < 3

Если описывать его ход словами, то здесь нужно будет сказать, что переменная x может быть положительной, равной нулю или отрицательной, а затем рассмотреть отдельно случаи для x ≥ 0 и для x < 0 .

Если принять, что x ≥ 0, то |x| = x и неравенство |x| < 3 можно тогда представить в виде

x < 3

Таким образом получаются два математических выражения (x ≥ 0 и x < 3), которые требуют их одновременного выполнения, следовательно, их возможно записать так:

Если же выражение под модулем отрицательное (x < 0), то по аналогии с предыдущим случаем это следует изобразить следующим образом:

Присмотримся ко второму неравенству получившейся системы: –x < 3 . Как известно, его смысл нисколько не поменяется, если поделить обе его части на –1 , не забыв при этом поменять знак неравенства с «меньше» на «больше». Нетрудно догадаться, что такое действие может быть записано так:

–x < 3 ⇔ x > –3 ,

из чего становится не требующей пояснений следующая запись:

Рассмотрение разных знаков x возможно описать компактно и без лишних слов при помощи символа объединения:

Посудите сами – такая запись охватывает все возможные значения переменной: « x ≥ 0 ИЛИ x < 0 ». Применительно к исходному неравенству всё сказанное означает, что оно может быть представлено в виде равносильной ему конструкции, описывающей рассмотрение случаев разных знаков подмодульного выражения и представляющей объединение двух систем, с которым дальше также проводятся равносильные преобразования:

Здесь: (1) – рассмотрение случая для неотрицательных значений подмодульного выражения; (2) – вариант, когда величина под модулем принимается меньшей нуля; (3) – изменение во втором неравенстве системы знака перед x на обратный; (4) – запись получившихся систем в виде соответствующих двойных неравенств; (5) – объединение («слияние») полуинтервала и интервала значений x в один интервал, тоже описываемый двойным неравенством, которое уже можно считать решением исходного неравенства.

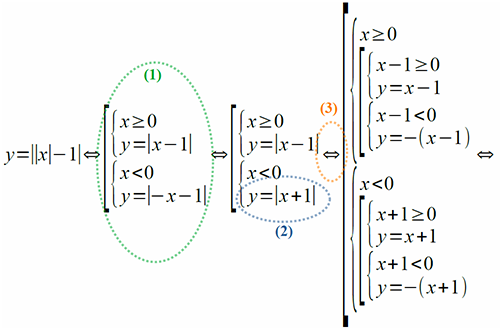
Вот теперь, когда начальные пояснения о равносильных преобразованиях и форме их записи даны, можно приступать к обещанному в начале.

Проведём с выражением функции необходимые равносильные преобразования:

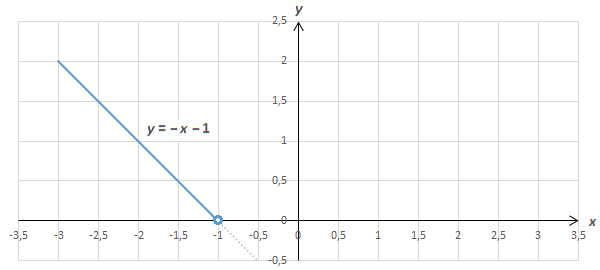
Согласен, что выглядит это всё пугающе, но уверяю – бояться не стоит, здесь можно разобраться, если захотеть. Как и в случае с решением неравенства |x| < 3, объединение двух систем (1) представляет собой раскрытие внутреннего модуля в выражении функции. В уравнении (2) сделана замена в соответствии с тождеством |–a| = |a| . Сразу после (3) расписано раскрытие ещё одного, внешнего, модуля. Пожалуй, наиболее сложным и непонятным представляется переход (4), поэтому он заслуживает отдельного комментария и для удобства объяснения каждому математическому высказыванию (неравенству или уравнению функции) перед (4) присвоено условное буквенное обозначение. Ранее упоминалось, что символ системы (фигурная скобка) работает подобно союзу «И», а объединение (квадратная скобка) – подобно союзу «ИЛИ». Теперь пришла пора добавить к сказанному, что «И» выполняет роль логического умножения, а «ИЛИ» – логического сложения. С учётом этого всю совокупность выражений перед (4) можно формально описать следующим образом:

( A·(B·C + D·E) ) + (F·(G·H + I·J) )

Данное описание также формально можно преобразовать как обычное алгебраическое – раскрыть в нём скобки:

( A·(B·C + D·E) ) + ( F·(G·H + I·J) ) =
= ( A·B·C + A·D·E ) + ( F·G·H + F·I·J ) =
= A·B·C + A·D·E + F·G·H + F·I·J

Думаю, что теперь стало ясно, почему при рассматриваемом переходе (4) совокупность математических выражений представляется в виде объединения четырёх систем.

В итоге после раскрытия модулей стало очевидным, что множество значений переменной x разбивается на четыре участка, в каждом из которых график функции y = | |x| – 1 | совпадает с графиком определённой линейной функции:

1. При x < –1 это график функции y = –x – 1:

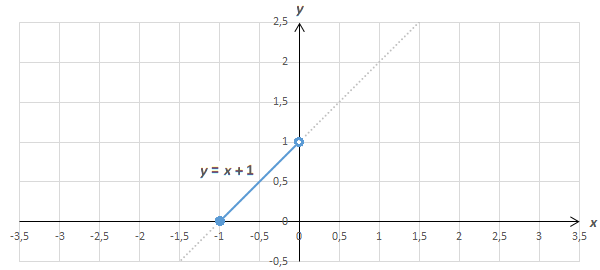
2. При –1 ≤ x < 0 это график функции y = x + 1:

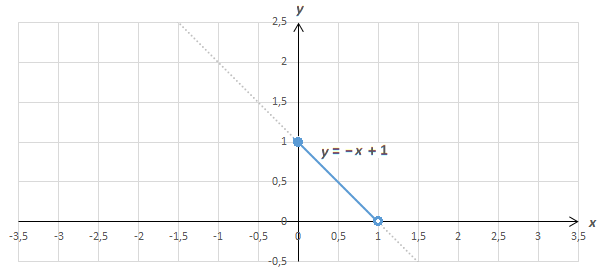
3. При 0 ≤ x < 1 это график функции y = –x + 1:

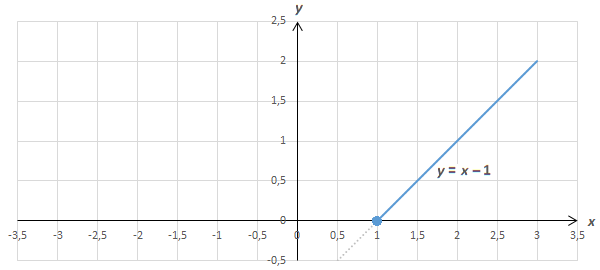
4. При x ≥ 1 это график функции y = x – 1:

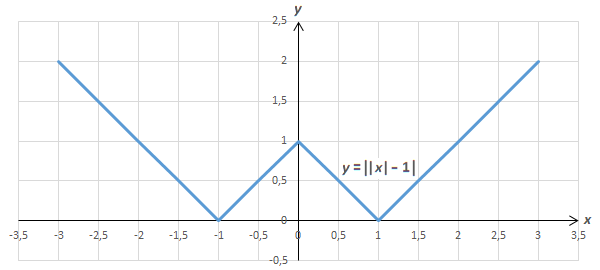
Конечный результат представляет собой объединение приведённых четырёх фрагментов, образующих непрерывную ломанную линию, похожую на латинскую букву “W” (у меня, правда, вид графика ассоциируется с созвездием Кассиопеи):

Разумеется, строить график рассмотренной функции проще другим путём – взять график функции y = x , зеркально отразить относительно оси абсцисс его часть, лежащую ниже этой оси на полуплоскость положительных значений y (при этом выйдет график функции y = |x| в виде «галки»), затем сдвинуть вниз на единицу вдоль оси ординат (то есть изобразить график функции y = |x| – 1), а потом ту его часть, оказавшуюся ниже оси абсцисс («носик» «галки»), снова отразить вверх, на положительную полуплоскость, получив такую же ломаную, что и на последнем рисунке. Здесь нужно напомнить, что цель данной заметки заключалась в рассказе о довольно компактном способе записи всех необходимых выкладок и преобразований, которые приходится выполнять с математическими выражениями и при решении других задач.

Хочется надеяться, что разъяснения получились достаточно понятными (для любопытных школьников, прежде всего), и что я в них не ляпнул чего-нибудь крамольного и способного вызвать праведный гнев у людей, лучше меня разбирающихся в математике – было бы интересно услышать от них отзывы о данном опусе.

Добавлено: 29.12.2021

Изменено: 29.12.2021

Скачать в pdf