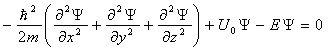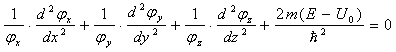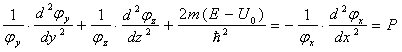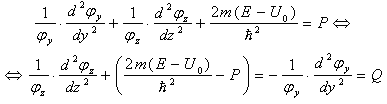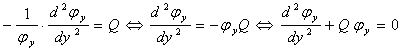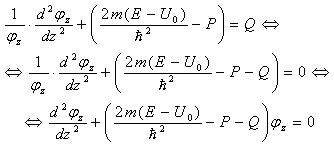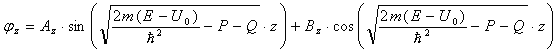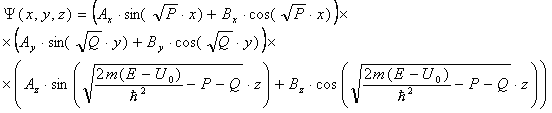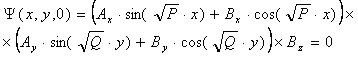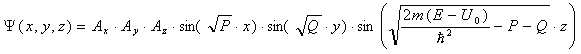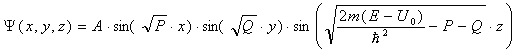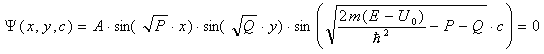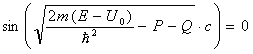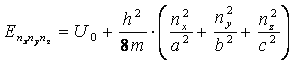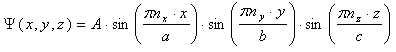История возникновения представленного ниже материала такова. На втором курсе нам читали лекции по квантовой химии. Естественно, когда на них зашла речь об уравнении Шрёдингера, не обошлось без записи его применительно к движению электрона в атоме водорода. Как я тогда понял, общий подход к решению уравнения таков. Поскольку в нём в качестве неизвестного выступает функция нескольких независимых переменных, то уравнение преобразуется так, что из него получаются несколько уравнений, каждое из которых содержит только какую-то переменную (эта процедура называется разделением переменных). Далее каждое из полученных уравнений решается отдельно и полученные решения потом объединяются.

Уравнение Шрёдингера для атома водорода было записано в декартовых прямоугольных координатах и было объявлено, что в такой записи разделить переменные в нём (и, соответственно, решить его) невозможно и для решения нужно перейти к сферическим координатам. Именно эту задачу – перейти в уравнении Шрёдингера для атома водорода к сферической системе координат и произвести разделение переменных, получив из одного дифференциального уравнения три – лектор (д. х. н., профессор Олейник А. В.) оставил нам в качестве дополнительного задания к экзамену.

Когда началась сессия и предстояло подготовиться к экзамену, я добросовестно выполнил задание, однако получившиеся уравнения были довольно сложны – моих знаний по математике было явно недостаточно для их решения, то есть получить конечный результат – выражение для волновой функции электрона в атоме водорода – я бы не смог. Вот тогда-то мне и пришла в голову идея рассмотреть более простой случай, представленный здесь.

Несмотря на то, что этот случай является чисто гипотетическим, он позволяет получить представление о том, откуда берутся квантовые числа, с помощью которых описывается состояние электронов в атомах, и понять, что эти квантовые числа являются следствием решения волнового уравнения для реального атома. При этом чтобы понять сам процесс решения не обязательно знать всю теорию дифференциальных уравнений от "а" до "я", а достаточно лишь иметь представление о том, что такое частная производная функции нескольких переменных и что такое дифференциальное уравнение второго порядка.

Пусть электрон находится внутри области, имеющей вид прямоугольного параллелепипеда с измерениями a, b и c (см. рисунок), причём потенциальная энергия электрона внутри этой области равна U=U0 (U0 – конечная постоянная величина), а на границаx и за её пределами U = + ∞. Задача: для случая консервативной системы (т. е. системы не изменяющейся во времени) найти для электрона выражение волновой функции, описывающей его движение в указанной области, и выражение для полной энергии.

Для удобства дальнейшего изложения материала необходимо сделать два примечания.

Примечание а). Рассмотрим дифференциальное уравнение следующего вида (уравнение незатухающих гармонических колебаний):

Общее решение этого уравнения обычно записывают так:

где А и B – произвольные постоянные.

Примечание б). Рассмотрим интеграл от функции

на отрезке [0, l].

Если n – натуральное число, то

Для консервативной системы уравнение Шрёдингера, описывающее движение электрона, имеет следующий вид:

Здесь: m – масса электрона, – приведённая постоянная Планка (h/2π), Е – полная энергия электрона. Волновая функция Ψ=Ψ(x, у, z) в силу того, что за пределами рассматриваемой области U = +∞, должна быть равной нулю во всеx точкаx, не принадлежащих этой области. Kроме того, в этом случае из требования непрерывности волновой функции вытекает, что Ψ должна быть равна нулю и на границаx области. Исходя из этого можно записать граничные условия для этого случая:

Запишем уравнение Шрёдингера для нашей задачи:

Поделим обе части уравнения на

и вынесем за скобки Ψ:

Необходимо отметить, что функция Ψ=0 является решением уравнения (10) – это так называемое тривиальное решение, однако для решения поставленной задачи нас интересует нетривиальное решение – его-то и нужно отыскать. Так как Ψ не зависит от времени (система консервативна), то выражение для волновой функции будем отыскивать в виде произведения трёх функций, каждая из которых зависит только от одной переменной:

B этом случае:

Подставим (11), (12), (13) и (14) в (10), после чего поделим обе части (10) на φ_x·φ_y·φ_z. Получим:

B полученном выражении перенесём слагаемое

:

Левая часть (15) зависит от у и z, а правая часть зависит от x. Это говорит о том, что правая и левая части (15) равны некоторому постоянному числу Р. Из (15):

Уравнение (16) с точностью до обозначений совпадает с (1), поэтому общее решение (16) выглядит так (А_x и B_x – произвольные постоянные):

Вернёмся к (15):

B (18) левая и правые части зависят соответственно только от z и только от у, поэтому как в предыдущем случае они равны некоторому постоянному числу Q. Из (18):

Общее решение (19) есть (A_y и B_y – произвольные постоянные):

Далее:

Для (21) общее решение выглядит так (A_z и B_z – произвольные постоянные):

Объединяя (17), (20) и (22) получаем общее решение уравнения (10):

Для выделения частного решения, удовлетворяющего граничным условиям, используем выражения (4)-(9).

Пусть z=0, тогда из (6) следует что

Так как выражения

и

в общем случае не равны нулю (иначе имело бы место тривиальное решение уравнения (10)), то для того, чтобы условие (6) выполнялось при любых x и у необходимо, чтобы B_z было равным нулю: B_z=0. Аналогично из условий (4) и (5) следует, что B_x=0 и B_y=0. Волновая функция запишется теперь в виде:

Обозначим A=A_x·A_y·A_z:

Пусть теперь z=с (условие (9)), тогда:

А≠0, так как получится тривиальное решение, а множитель опять же в общем случае не равен нулю, поэтому для выполнения условия (9) нужно, чтобы выполнялось равенство:

Это возможно, если

,

где n_z – натуральное, так как значение квадратного корня больше нуля и с>0. Следовательно:

Аналогично из условий (7) и (8) следует, что (n_x и n_у – натуральные):

Возведём (26) и (27) в квадрат, подставим в (25), после чего (25) тоже возведём в квадрат:

Выразим из (28) Е:

Из этого выражения как раз и следует, что полная энергия электрона может принимать только дискретные значения, определяемые тремя натуральными числами n_x, n_y, n_z (квантовыми числами).

Волновую функцию теперь можно записать так:

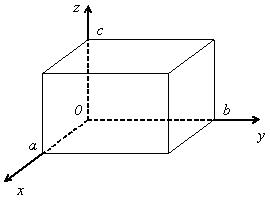
Определим, чему равна константа А в (29). Условие нормировки волновой функции:

,

где V – всё пространство. Для нашего случая можно записать:

,

где V₁ – часть пространства, ограниченная рассматриваемым прямоугольным параллелепипедом с измерениями a, b, c, а V₂ – всё остальное пространство, причём:

,

следовательно:

Подставляем (29) в (30):

Используя (3) можно записать:

Отсюда

.

Подведём итог. Волновая функция, полностью удовлетворяющая условиям задачи, имеет вид:

Полная энергия электрона определяется следующим выражением:

B выражениях (I) и (II) n_x, n_y, n_z – натуральные числа.

Как видно из вышеизложенного, в процессе решения уравнения Шрёдингера как бы сами собой выплывают три натуральных числа, значения которых однозначно определяют выражение для волновой функции, описывающей движение электрона внутри рассматриваемой области, и значение энергии, которой может обладать электрон в данном случае. Эти три натуральных числа и будут для нашего рассмотренного примера являться квантовыми числами. Из полученных результатов можно сделать следующие выводы.

Во-первых, энергия электрона, находящегося внутри рассматриваемой области, как это следует из (II), может принимать лишь определённый (дискретный) набор значений и меняться может лишь скачками, а не непрерывно.

Во-вторых, оказывается, что число квантовых чисел, необходимых для описания каждого из возможных энергетических состояний равно числу независимых координат (в нашем случае их три, так как рассматривается трёхмерное пространство). Если бы мы стали рассматривать случай одномерной или двухмерной бесконечно глубокой потенциальной ямы, то для описания энергетического состояния электрона (как это бы выяснилось при решении уравнения) было бы нужно одно или два квантовых числа соответственно.

Последнее утверждение может показаться непонятным, ведь состояние электрона в атоме описывается не тремя, а четырьмя квантовыми числами, причём значения орбитального квантового числа зависят от величины главного квантового числа, а значения магнитного квантового числа находятся в зависимости от значения орбитального. Из результатов, полученных выше, следует, например, что значение n_у никак не зависит от n_x и n_z. Всё дело в том, что при постановке и решении нашей задачи никак не учитывалась природа самой частицы и движение её рассматривалось в отсутствие полей, которые обязательно должны были бы повлиять на его характер. B нашем случае исходному уравнению "безразлично", что именно находится в нашей "яме": электрон, протон или какая-нибудь другая частица – на конечный вид выражения волновой функции и выражения для энергии это не влияет. B реальном атоме электроны движутся во внешнем электрическом поле, создаваемом атомным ядром и другими электронами этого атома, а "выход на сцену" четвёртого, спинового, квантового числа обусловлен наличием у электрона такого свойства как спин.

Добавлено: 16.01.2006

Изменено: 07.01.2010

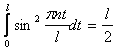Скачать в pdf